In questo articolo andremo a parlare del metodo di Cross per la risoluzione di strutture iperstatiche in pochi minuti.
Il metodo di Cross è un’evoluzione del metodo delle deformazioni, che permette di risolvere strutture con un alto numero di grado di iperstaticità.
Le strutture iperstatiche sono le strutture che hanno un numero di gradi di vincoli maggiore del numero dei gradi di libertà.
I gradi di libertà, per le strutture bidimensionali, sono tre ovvero due traslazioni (verticale e orizzontale) e una rotazione.
I gradi di vincolo dipendono dalla tipologia di vincolo applicato, in parole semplici i gradi vincolo rappresentano il numero degli spostamenti impediti dai vincoli.
Normalmente quando il numero dei gradi di libertà eguaglia il numero dei gradi di vincolo si parla di strutture isostatiche, mentre quando i gradi di libertà sono maggiori dei gradi di vincolo le strutture sono labili, infine nel caso rimanente, i gradi di libertà sono minori dei gradi di vincolo, si parla di strutture iperstatiche.
Al fine di definire completamente le strutture isostatiche sono sufficienti solo le equazioni di equilibrio, mentre per le strutture iperstatiche bisogna fare affidamento anche su altri metodi, come, per esempio, il metodo di Cross.
Al fine di spiegare al meglio il metodo di Cross per la risoluzione di strutture iperstatiche, si valuta la seguente struttura:
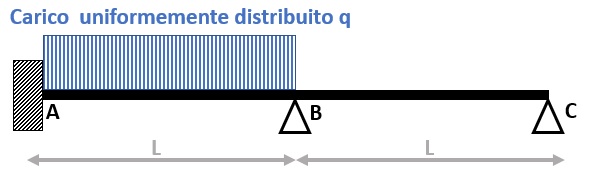
La struttura presenta 3 gradi di libertà e 5 gradi di vincolo, infatti:
Gradi di vincolo: 3 (incastro in A) + 2 (cerniera in B) +2 (cerniera in C)
Di conseguenza:
3 gradi di libertà < 5 gradi di vincolo la struttura è iperstatica.
Inoltre, la struttura è costituita da un materiale elastico lineare e la sua sezione si mantiene costante lungo tutta la lunghezza.
La fase successiva consiste nel valutare le rigidezze delle aste AB e BC, infatti si ha:
L’asta AB ha rigidezza pari a 4 EJ/L.
L’asta BC ha rigidezza pari a 3 EJ/L.
Dove:
E il modulo elastico;
J è il momento di inerzia;
L è la lunghezza dell’asta.
Le rigidezze dipendono dalla tipologia di vincolamento a cui sono sottoposte le aste, infatti un’asta appoggio-appoggio ha sempre rigidezza pari a 3 EJ/L, mentre un’asta appoggio-incastro ha una rigidezza pari a 4 EJ/L.
Successivamente si blocca il nodo B con un morsetto e si evidenziano i momenti di reazione, quest’ultimi si ricavano da un prontuario in quanto schemi noti.
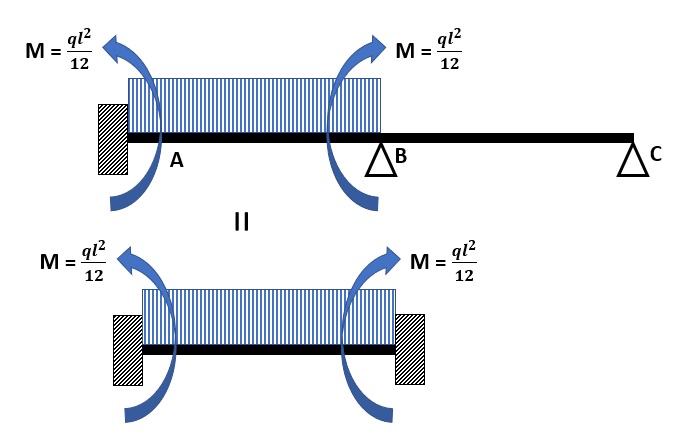
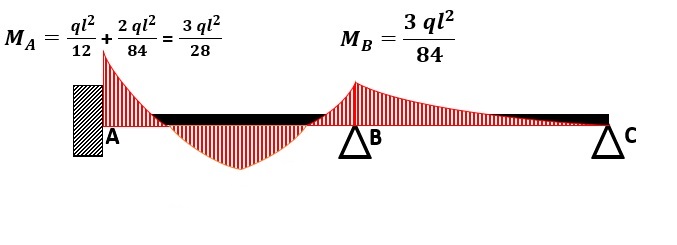
Al fine di rendere agevole la lettura si pone M uguale a ql2/12.
Svolto questo passaggio si ripartisce M in proporzione alle rigidezze delle aste convergenti al nodo B.
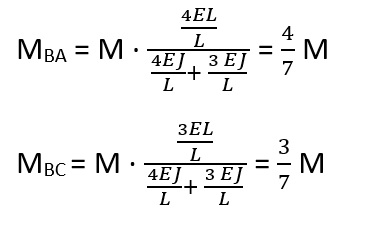
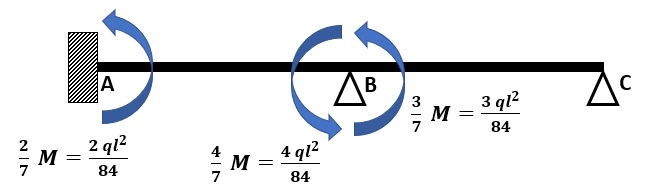
Infine, si sfrutta la sovrapposizione degli effetti, essendo il materiale elastico lineare, sommando i momenti di reazione (ql2/12) con i momenti appena trovati.
Si ricava quindi il seguente diagramma del momento flettente: