In questo articolo andremo a vedere come utilizzare il metodo delle forze per la risoluzione di strutture iperstatiche.
Le strutture iperstatiche sono le strutture che posseggono un numero di gradi di vincolo maggiore del numero dei gradi di libertà.
I gradi di libertà, nel piano, sono tre, ovvero due traslazioni (verticale e orizzontale) e una rotazione.
Per la risoluzione della struttura, in particolare per determinare le reazioni vincolari, si possono impiegare le equazioni di equilibrio:
- Equilibrio delle azioni orizzontali;
- Equilibrio delle azioni verticali;
- Equilibrio dei momenti.
In aggiunta a queste equazioni, nelle strutture iperstatiche, si possono aggiungere delle altre, affinché il numero delle incognite eguagli il numero delle equazioni disponibili, rendendo il sistema risolvibile.
Queste equazioni aggiuntive si chiamano equazioni di congruenza.
Il metodo delle forze viene impiegato per la determinazione di tali equazioni aggiuntive, infatti esse si ricavano ponendo come incognite le reazioni vincolari sovrabbondanti e imponendo che la struttura si deformi rispettando la congruenza dei vincoli interni ed esterni.
Per chiarire meglio l’applicazione si esegue il seguente esercizio dimostrativo, che consiste nel trovare le reazioni vincolari della seguente struttura.
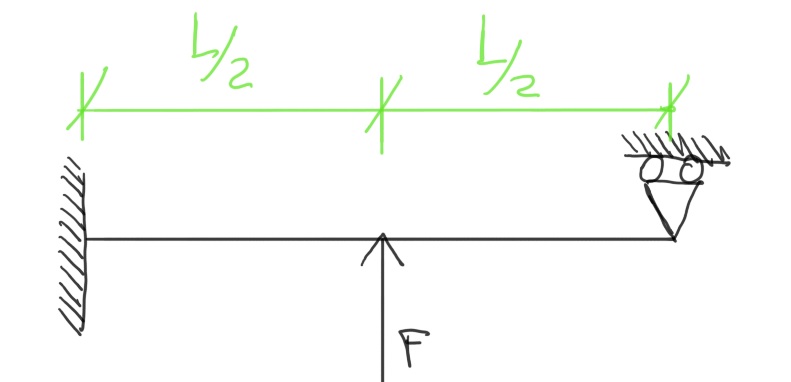
Il materiale impiegato è isotropo, omogeneo e con un comportamento elastico lineare.
La struttura presenta 3 gradi di libertà, essendo nel piano bidimensionale ( 2D ):
3 gradi di libertà = Spostamento verticale + spostamento orizzontale + rotazione
Con 4 gradi di vincolo:
4 gradi di vincolo = 3 (incastro) + 1 (carrello scorrevole)
Di conseguenza la struttura risulta essere una volta iperstatica:
4 gradi di vincolo – 3 gradi di libertà = 1
Svolto questo passaggio, si passa a definire l’incognita iperstatica, che nel caso in esame sarà la reazione verticale del carrello scorrevole.
Per poi sfruttare la sovrapposizione degli effetti, essendo il materiale elastico lineare, al fine di determinare gli spostamenti verticali nell’estremità a destra.
Si pone la congruenza e si ricava il valore della reazione iperstatica incognita X.
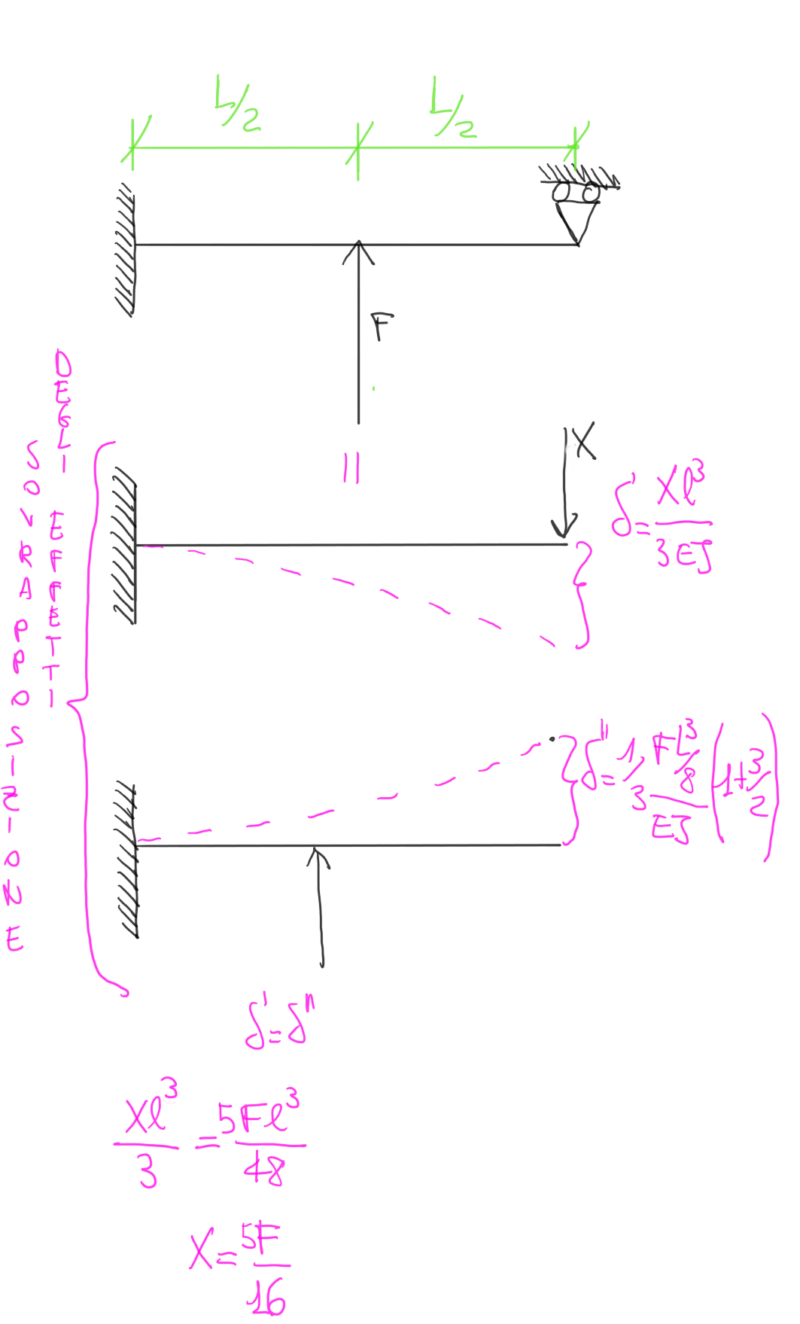
In questa sede, è opportuno ricordare che il momento sul carrello scorrevole risulta essere sempre nullo.
Bibliografia:
Erasmo Viola, Esercitazioni di Scienza delle costruzioni/2, Casa editrice Pitagora (Bologna), anno 1985.