In questo articolo andremo a trattare la risoluzione delle strutture isostatiche, fornendo gli strumenti base per determinare i diagrammi del momento flettente, del taglio e dello sforzo assiale.
Le strutture si definiscono isostatiche quando i gradi di libertà sono uguali ai gradi di vincolo, dove i gradi di libertà rappresentano i movimenti possibili di una struttura, mentre i gradi di vincolo sono gli spostamenti impediti dai vincoli.
Per strutture bidimensionali, tipicamente studiate nei corsi universitari di ingegneria, i gradi di libertà sono 3, ovvero un corpo nel piano bidimensionale ha i seguenti spostamenti:
- Spostamento verticale;
- Spostamento orizzontale;
- rotazione.
I gradi di vincolo rappresentano gli spostamenti impediti dai vincoli presenti nella struttura, per saperne di più clicca qui.
Per la risoluzione delle strutture isostatiche si utilizzano le tre equazioni di equilibrio, ovvero:
- Equazione equilibrio azioni verticali;
- Equazione equilibrio azioni orizzontali;
- Equazione equilibrio dei momenti flettenti.
Per spiegare meglio questi concetti ci si rifà al seguente esercizio che consiste nel trovare le reazioni vincolari, il diagramma del momento e del taglio.
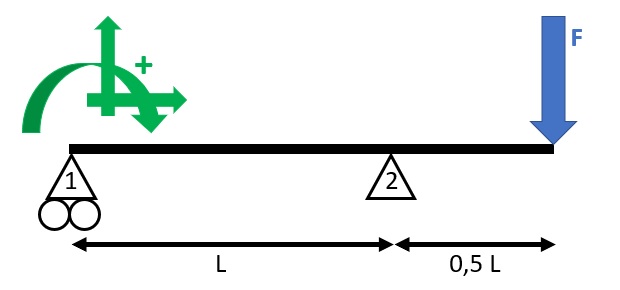
Per prima cosa si scrive l’equazione di equilibrio delle azioni verticali:
V1 + V2 – F = 0
Le incognite sono le reazioni vincolari V1 e V2, mentre non sono presenti azioni orizzontali. Si scrive ora l’equilibrio ai momenti flettenti rispetto al polo 1:
F ∙ 1,5 L – V2 ∙ L = 0
Da cui si ricava che:
V2 = 1,5 F
Di conseguenza, dall’equazione di equilibrio delle azioni orizzontali si ha:
V1 = – 0,5 F
Si può quindi iniziare a disegnare il diagramma del taglio prendendo in considerazione la relativa convenzione data dal concio elementare:
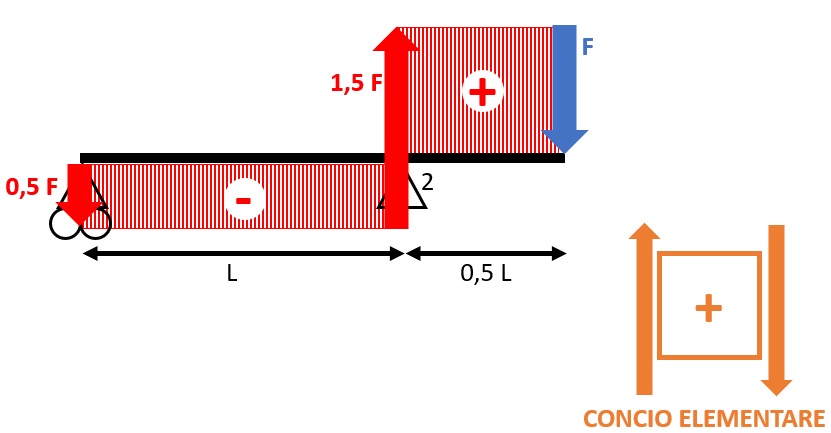
Nel tratto 1-2 le reazioni vincolari V1 e V2 non sono concordi con il concio elementare quindi il taglio è negativo.
Lo sbalzo ha invece le forze all’estremità, V2 e F, concordi con il concio elementare, di conseguenza, il taglio è positivo.
Per quanto riguarda il diagramma del momento flettente, si utilizza la convenzione secondo la quale il momento che tende le fibre inferiori viene definito positivo.
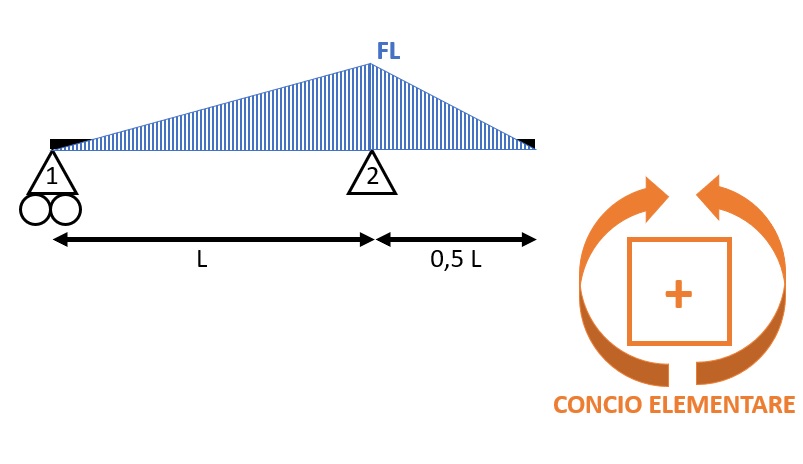
Il momento massimo si trova sopra il vincolo 2 è vale F ∙ L, in quanto sullo sbalzo è solo presente la forza F.