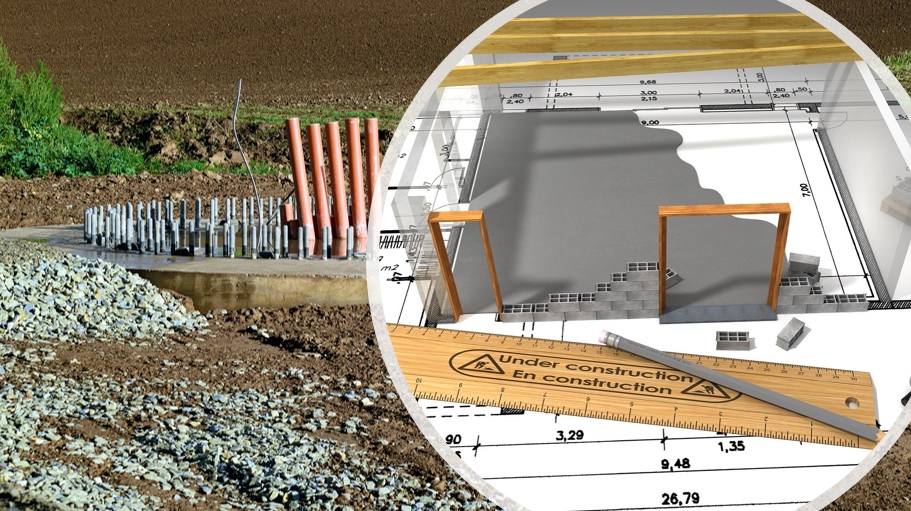
In questo articolo andremo a definire i criteri progettuali delle travi rovesce in cemento armato in funzione di quanto scritto nelle norme tecniche per le costruzioni (NTC 2018).
Le travi rovesce sono una tipologia di fondazione superficiale, impiegata molto spesso negli edifici in cemento armato, quando terreni hanno buone caratteristiche meccaniche già alle basse profondità.
Per valutare i criteri progettuali delle travi rovesce in cemento armato è necessario tenere conto dei seguenti aspetti:
- Materiale da costruzione;
- Sezione trasversale della sezione della trave;
- Numero e tipologia dei vincoli;
- Tipologia del terreno;
- Tipologia delle sollecitazioni a cui è sottoposta.
In genere, le travi rovesce sono delle fondazioni superficiali con uno sviluppo lineare, aventi una sezione a T rovescia, da cui il nome.
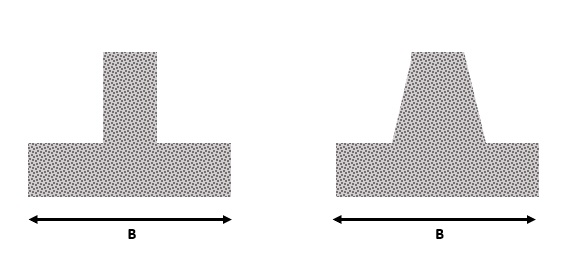
Normalmente impiegate, in ambito edilizio, per avere una maggiore superficie di contatto rispetto ai plinti di fondazione.
Il metodo semplificato, per analizzarle, prevede le seguenti ipotesi:
- Sovrastruttura a vincoli fissi;
- Modello di terreno di tipo elastico.
La prima ipotesi permette di evitare l’analisi dell’interazione fondazione-sovrastruttura, mentre la seconda ipotesi permette di semplificare l’analisi dell’iterazione fondazione terreno, utilizzando i seguenti modelli:
- Modello di semispazio elastico;
- Modello di Winkler.
I due modelli risultano avere risultati apprezzabili quando i carichi sono di tipo concentrato (forze o/e momenti), mentre per carichi distribuiti il Modello di Winkler è sconsigliato.
Il modello di Winkler parte dall’equazione differenziale della trave inflessa:
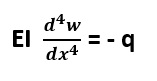
Dove:
E il modulo elastico del materiale da costruzione;
I è il momento di inerzia;
w è lo spostamento;
q è la pressione di contatto.
Il suolo viene schematizzato come un letto di molle, dove vi è una relazione lineare, tra il carico applicato e il relativo cedimento.
q’ = q ∙ K
L’equazione differenziale elastica diventa quindi:
E ∙ I ∙ wIV + K ∙ B ∙ w=0
Da cui si ricava l’espressione generale di w:
w = eλx ∙ [C1 sin (λx) + C2 sin (λx)] + e-λx ∙ [C3 sin (λx) + C4 sin (λx)]
Dove C1, C2, C3 e C4 si determinano imponendo le condizioni al contorno.
Noto w, si ottiene l’andamento del momento e del taglio:
M = EI d2w/dx2
V = EI d3w/dx3
Bibliografia:
Vincenzio Nunziata, Teoria e pratica delle strutture in cemento armato, Dario Flaccovio editore, anno 2014